1. Introduction A highly successful mathematical
theory of spin has already been developed by P.A.M. Dirac and others (Eisele, 1960). It predicted the discovery of the positron (Anderson, 1922) and correctly gave the value of the spin, h/4pi angular momentum
units. Prior to this paper, there has been no successful physical
description of spin or any suggestion of its origin, although it was recognized to be a quantum phenomenon. The electron's structure, as well as its spin, had been a mystery. Providing a physical origin of spin for the first time is the purpose of this paper.
In Dirac's theoretical work the spin of a particle is measured in units of angular momentum, like rotating objects of human size. But particle spin is uniquely a quantum phenomenon, different than human scale
angular momentum. Its value is fixed and independent of particle mass or angular velocity. However, spin properties are found to be related to other properties of the electron's quantum wave function;
that is, mirror or parity inversion (P), time inversion (T), and charge inversion (C). For example, the quantum operation CPT on a particle is found to be invariant,CPT= {C
harge inversion} x {Parity inversion} x {Time inversion} = an invariant This study returns to a proposal that was popular sixty years ago among the pioneers of quantum theory: namely
that matter consisted of wave structures in space. Thus, it was proposed that matter substance, mass and charge, did not exist but were properties of the wave structure. Wyle, Schroedinger, Clifford, and
Einstein were among those who believed that particles were a wave structure. Their belief was consistent with quantum theory, since the mathematics of quantum theory does not depend on the existence of particle
substance or charge substance. In short, they proposed that quantum waves are real and mass/charge were mere appearances; 'Schaumkommen' in the words of Schroedinger. The reality of quantum waves, as
suggested by Cramer (1986), supports the original concept of W. K. Clifford (1876) that all matter is simply "undulations in the fabric of space."
Wheeler and Feynman (1945) first modeled the electron as spherical inward and outward electromagnetic waves seeking the response of the universe (from other matter) to explain radiation, but encountered
difficulties because there are no spherical solutions of the electromagnetic equations using vector fields. Cramer (1986) discusses the response
for real quantum waves. Using a quantum wave equation (scalar fields) and spherical quantum waves, Wolff (1990, '91, '93, '95, '97) found and described a wave structure of matter which successfully predicted the Natural Laws as experimentally measured. It has predicted all of the properties of the electron except one - its spin. Now, this paper completes those predictions with a physical origin of spin that is in accord with quantum theory, the Dirac Equation, and the previous structure of the electron.
Briefly summarizing Wolff, the electron is comprised of two spherical scalar waves, one inward and one outward. These waves are superimposed at the origin with opposite amplitudes, as shown in Figure 1in the
next section, to form a single resonant standing wave
in space centered at the electron's location. A reversal of the inward wave occurs at the center where r = 0. Spin appears as a required rotation of the inward wave to become the outward wave. The outward wave induces a
response of the universe
when it encounters other matter in its universe and modulates their outward waves. The tiny Huygens components of those waves return to the center and become the inward wave. This simple structure, termed a
space resonance (SR), produces all experimental properties of electrons. This structure, the electron properties, and the laws of nature originate from three basic principles or assumptions. No
other laws are required as these principles are the origin of the laws of nature. Briefly they are:
Principle I. A Wave Equation
. Determines the behavior of quantum waves.Principle II. Wave Density Principle. A quantitative generalization of Mach's principle, which determines the density of the quantum wave medium.
Principle III. Minimum Amplitude Principle (MAP). The sum of wave amplitudes seeks a minimum at each point.
The following wave equation is the First Principle.
2. Wave Structure of the Electron The structure of the electron consists of solutions of a general wave equation (Wolff, 1990). This
equation governs the behavior of all particle waves in space, and is:
(grad)2(AMP) - (1/c2) d 2
(AMP)/ dt2= 0
[1]
where AMP is a scalar amplitude, c is the velocity of light, and t is the time. These waves are scalar quantum waves, not electromagnetic waves. This wave equation has two spherical solutions for the
amplitude of the electron: one of them is an inward wave converging to the center; the other is a diverging outward wave. The two solutions are:
{IN-amplitude} = (1/r) {AMP-max} exp(iwt + ikr)
{OUT-amplitude} = (1/r) {AMP-max} exp(iwt - ikr) [2]
where:
w = 2pi mc2/h = the angular frequency
k = 2pi/{wave length} = the wave number. The inward wave converges to its
center and rotates to become a diverging outward wave. The superposition of the continuous inward and outward waves forms the electron, Figure 1, and is termed a space resonance. To transform the
inward wave to an outward wave and obtain constructive interference with proper phase relation requires a rotation and phase shift at the center. This rotation produces a spin value h/4pi, the same for all charged
particles because all particles propagate in the same universal wave medium.
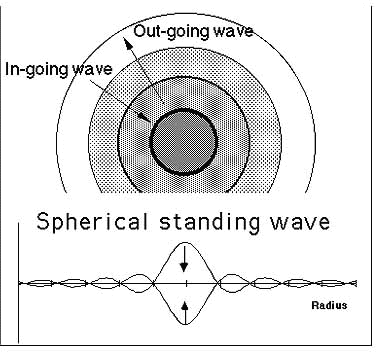
|
Figure 1. Electron Structure. The upper diagram shows a
cross-section of the spherical wave structure, something like the layers of an onion. It is comprised of an inward moving wave and an outward moving wave. The two waves combine to form a single
dynamic standing wave structure with its center as the nominal location of the electron. Note that the amplitude of a quantum wave is a scalar number, not an electromagnetic vector. Thus these
waves are part of quantum theory, not electric theory. At the center the quantum wave amplitude (and the electric potential) is finite, not infinite, in agreement with the observed electron (Wolff,
1995). The lower diagram shows the same quantum wave amplitude plotted along a radius outwards from the electron center. The lower diagram is a 'slice' from the upper diagram. |
3. Spherical Rotation
Rotation of the inward quantum wave at the center to become an outward wave is an absolute requirement to form a particle
structure. Rotation in space has conditions. Any mechanism that rotates (to creates the quantum "spin") must not destroy the
continuity of the space. The curvilinear coordinates of the space near the particle must participate in the motion of the particle. Fortunately, nature has provided a way - known as spherical rotation -
a unique property of 3-D space. In mathematical terms this mechanism, according to the group theory of 3-D space, is described by stating that the allowed
motions must be represented by the SU(2) group algebra which concerns simply-connected geometries.
Spherical rotation is an astonishing property of 3-D space. It permits an object structured of space to rotate about any axis
without rupturing the coordinates of space. After two turns, space regains its original configuration. This property allows the
electron to retain spherical symmetry while imparting a quantized "spin" along an arbitrary axis as the inward waves converge
to the center, rotate with a phase shift to become the outward wave, and continually repeat the cycle. The required phase shift is a 180o
rotation that changes inward wave amplitudes to become those of the outward wave. There are only two possible directions of rotation, CW or CCW. One choice is an electron with spin of +h/4pi, and the
other is the positron with spin of -h/4pi. It is an awesome thought that if 3-D space did not have this geometric property of spherical rotation, particles and matter as we know them could not exist.
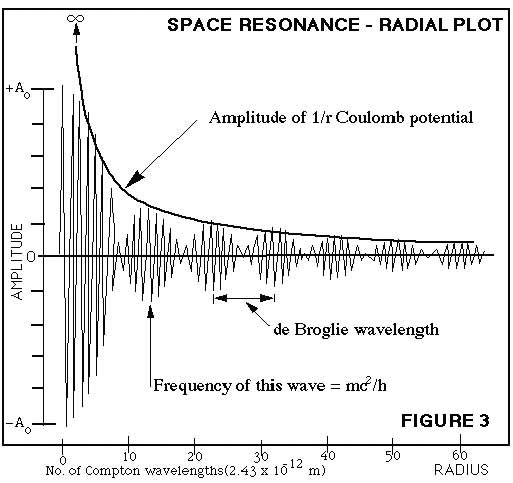
|
Figure 2. Radial Plot of the Electron Structure.
When the IN and OUT quantum waves combine they form a standing wave. This detailed plot, the same as the approximate lower plot of Fig. 1 above, corresponds exactly to the equations below. The envelope of the wave amplitude matches the Coulomb potential everywhere except at the center, where it is not infinite in agreement with the observations of Lamb and Retherford. If the electron were moving and observed by another detector atom with relative velocity v, the deBroglie wavelength appears as a Doppler effect on
both waves. The frequency mc2/h of the waves was first proposed by Schroedinger and deBroglie, proportional to the mass of the electron. This frequency
is the mass so that mass measurements are actually frequency measurements. There is no mass 'substance' in nature. |
|
4. Dirac Theory of Electron Spin
The newly discovered quantum mechanics of the 1920s began to be applied to the physics of particles, seeking to further understand particles. Nobel Laureate P A.M. Dirac sought to find a relation between quantum
theory and the conservation of energy in special relativity given by
E2 = p2c2 + mo2c4 [3] He speculated that this energy equation might be converted to a
quantum equation in the usual way, in which energy E and momentum p are replaced by differential calculus
operators: E = (h/i) {d AMP/dt} and
p = h{d AMP/dx} + .. etc.
[4]
He hoped to find the quantum differential wave equation of the particle. Unfortunately, Eqn [3] uses squared terms and Eqn [4] cannot. The road was blocked!
Dirac had a crazy idea, "Let's try to find the factors of Eqn [3] without squares, by writing a matrix
equation"
[Identity]E = [alpha]pc + [beta]moc2
[5]
where: [Identity] is the identity matrix.
[alpha] and [beta] are new matrix operators of a vector algebra.
Dirac was lucky! He found that if [alpha] and [beta] were 4-vector matrices then Eqn [5] works okay. It is the famous
Dirac Equation. Eqns [4] and [5] can now be combined to get [Identity] (ih) d[AMP]/dt = (ch/i) {[alpha-x] d[AMP]/dx + [alpha-y] d[AMP]/dy +
[alpha-z] d[AMP]/dz + [beta]moc2[AMP]}
In general, [AMP] is a 4-vector: [AMP] = [AMP1, AMP2, AMP3, AMP4]. For the electron, this reduces to: [AMP] = [0, 1, AMP3(E,p) , AMP4(E,p)]
Dirac realized that for an electron only two wave functions, AMP3 and AMP4, were needed. These predicted an electron and a positron of energy E with spin
E = ± mc2 and spin = ± h/4pi
The positron was discovered five years later by Anderson (1931). Dirac simplified the matrix algebra by introducing 2-vectors (number pairs) which he termed 'spinors.' Spin matrices, which
operate on the vectors, were defined as follows:
{spin-x} = |
0 11 0 |
{spin-y} = |
0 i -i 0 |
{spin-z} = |
1 00 -1 |
{identity} = |
1 00 1 |
Thus Dirac had created a two-number algebra to describe particles instead of our common single number algebra. This
'spinor' algebra, while eminently successful, was entirely theoretical and gave no hint of the physical structure of the electron.
Now, in this paper, it is seen that the inward-outward quantum waves are the physical structure which corresponds to the
Dirac spinor. The two waves form a Dirac spinor, as was shown by Battey-Pratt et al (1986). The two physical spinor elements of the electron, or any charged particle, are as follows:
[electron amplitude] = |
{IN-AMP}{OUT-AMP} |
= (1/r) {AMP-max} |
e(iwt + ikr)
e(iwt - ikr) [6] |
An easily read description of the algebra of the Dirac Equation is given in Eisele (1960).5. Geometric Requirements of Electron Spin
Structuring particles out of space (the continuum) presents a problem if
the particles are considered free to spin. If part of the continuum is
part of the particle then another part of space would slide past the spinning
particle. As a result, the coordinate lines used to map out the whole space
would become twisted up and stretched without limit. The structure of space
would be torn or ripped so that one part of the continuum would slide past
another along a surface of discontinuity.
If you accept the philosophical position that "ripping of space" is
unacceptable, then you have to postulate that the mathematical groups of
the particle motion are simply connected and compact. In
this case the motion in the continuum will be cyclic and the configuration
of space can repeatedly return to an earlier initial phase. Does this occur
in nature? Yes, nature accommodates this requirement. Mathematicians have
long known of the spherical rotation property of 3D space in which
a portion of space can rotate and return identically to an earlier state
after two turns. This unusual motion was described in Scientific American
(Rebbi, 1979) and in the book Gravitation (Misner et al., 1973).
It is the basis of spin in this article.
What are the geometric requirements on the motion of a particle which
does not destroy the continuity of the space? The curvilinear coordinates
of the space near the particle must participate in the motion of the particle.
This requirement according to the group theory of 3D space is satisfied
by stating that the allowed motions must be represented by a compact simply-connected
group. The most elementary such group for the motion of a particle with
spherical symmetry is named SU(2). This group provides all the necessary
and known properties of spin for charged particles, such as the electron.
4. Understanding Spherical Rotation
This seldom studied motion can be modeled by a ball held by threads attached
to a frame. The threads represent the coordinates of the space and the
rotating ball represents a property of the space at the center of a charged
particle composed of converging and diverging quantum waves. The ball can
be turned about any given axis starting from any initial position. If the
ball is rotated indefinitely it will be found that after every two rotations
the system returns to its original configuration.
In the traditional analysis of rotating objects, it is usual to assume
that the process of inverting the axis of spin is identical to reversing
the spin. However, if the object is an electron which is continuously connected
to its environment as part of the space around it, this ceases to be true.
A careful distinction must be made between the inversion and the
reversal of particle spin. This distinction provides insight to
one of the most fundamental properties of particles.
To reverse the spin axis, one can reverse time ( t --> -t) or reverse
the angular velocity (w --> -w). Either are equivalent to exchanging the
outgoing spherical wave of an electron with the incoming wave. Then the
spinor becomes,
| {amplitude} = |
eiwt
0
|
-->
|
e-iwt
0
|
To invert the spin axis of the structure of the particle, it is necessary
to turn the structure about one of the axes perpendicular to the z spin
axis, for example the y axis. Then the inverted spin state is given by
the inversion matrix operation,
| {amplitude} = |
0 -1 eiwt
1 0 0
|
-->
|
0
eiwt
|
Thus, inversion and reversal are not the same. The difference between
these operations is characteristic of the quantum nature of the electron.
They are distinct from our human-sized view of rotating objects and are
important to understand particle structure.
5. The Group Mathematics of Spherical Rotation
Each configuration of the spherically rotating ball (or the electron center)
can be represented by a point on a Euclidean 4-D hypersphere which is also
the space of the SU(2) mathematics group. A rotation in the spherical mode
can be represented by any operator that will transform one vector into
another position. It is usual to assign the hypersphere a unit radius.
Then the rotations of the ball can be described by the mathematics of the
SU(2) group. It is also convenient to place the center of the unit hypersphere
at the origin and let the vector (1,0,0,0) represent an initial configuration
of the ball or electron. Any other configuration is often chosen with the
symbols (a,b,c,d). Then a2+ b2 +
c2 + d2 = 1.
A common representation for the hypersphere vectors is the quaternion
notation
{amplitude} = a +
ib + jc + kd
It can be shown (Battey-Pratt and Racey, 1986) that the 4x4 quaternion
operator is equivalent to a 2x2 operator as follows:
| {amplitude} = |
a + id c - ib
c + i a - id
|
where the matrix elements (often just 1, i, or 0) are now complex numbers.
You can see that the determinant of this is also a2 + b2
+ c2 + d2 = 1, as above. The spinor (operand) form
of (amplitude) is:
| {amplitude} = |
a + id
c + ib
|
This is the notation of the Spinors invented by Dirac to represent the
electron configuration, as shown in TABLE I. They also represent rotations
in the spherical mode which are members of the closed uni-modular SU(2)
group.
TABLE I: Properties of Spherical Rotation for
an electron in the SU(2) Representation
|
OPERATION
(Dirac symbol)
|
SU(2)
Operator
|
initial SU(2) Spinor
|
Final SU(2) Spinor
|
Equivalent Quaternion Operator
|
|
Leaves space as it is.
[Identity]
|
1 0
0 1
|
1
0
|
1
0
|
1
|
|
Rotates space 180o about the x-axis.
(spin-x)
|
0 i
i 0
|
1
0
|
0
i
|
i
|
|
Rotates space 180o
about the y-axis
(spin-y)
|
0 -1
1 0
|
1
0
|
0
1
|
j
|
|
Rotates space 180o
about the z-axis
(spin-y)
|
i 0
0 -i
|
1
0
|
i
0
|
k
|
For example, the spherical quantum waves in space can be rotated 180o
about the z axis by the operator (spin-z). If there is continuous rotation
of the quantum wave in space with angular velocity w, the spinor is represented
by
6. How Spin Arises from the Wave Structure of the Electron
The wave structure of the electron is composed of a spherical inward quantum
wave and an outward wave traveling at light speed c (Wolff, 1990, 1993,
1995). Figures 1 and 2 show the wave structure of an electron termed a
space resonance. The outward (OUT) wave of an electron travels to
and communicates with other matter in its universe. When these waves arrive
at other matter, a signature is modulated into their outward waves. These
outward-wave signatures are the response (Wheeler & Feynman,
1945; Cramer, 1986, Ryazanov, 1991) from the other matter. The total of
response waves from other matter in the universe, as a Fourier combination,
becomes the inward (IN) wave of the initial electron. The returned inward
waves converge to the initial wave center and reflect with a phase shift
rotating them to become the outward wave and repeating the cycle again.
The central phase shift is similar to the phase shift of light when
it reflects at a mirror. The required phase shift is a 180o rotation of
the wave, either CW or CCW. There are only two possible combinations
of the rotating inward and outward waves. One choice of rotation becomes
an electron, the other becomes a positron. The angular momentum change
upon rotation is either +h/4 or -h/4 . This is the origin of spin. One
wave set is the mirror image of the other set producing the CPT invariance
rule.
7. Conclusions
7.1. A COMPLETE SET OF ELECTRON PROPERTIES
The origin of spin completes the properties of the electron. All properties
can now be derived from the space-resonance structure and match all experimental
observations of the electron. There is now little doubt that matter is
composed of spherical quantum wave structures that obey the three principles
of wave structure of matter. But note that spin, and other properties,
are attributes of the underlying quantum space rather than of the individual
particle. This is why spin, like charge, has only one value for all particles.
The properties depend on the structure of space.
7.2. A UNIVERSE OF QUANTUM WAVES AND SPACE
Although the origin of spin has been a fascinating problem of physics for
sixty years, spin itself is not the important result. Instead, the most
extraordinary conclusion of the wave electron structure is that the laws
of physics and the structure of matter ultimately depend upon the waves
from the total of matter in a universe. Every particle communicates its
wave state with all other matter so that the particle structure, energy
exchange, and the laws of physics are properties of the entire ensemble.
This is the origin of Mach's Principle. The universal properties of the
quantum space waves are also found to underlie the universal clock and
the constants of nature.
This structure settles a century old paradox of whether particles are
waves or point-like bits of matter. They are wave structures in space.
There is nothing but space. As Clifford speculated 100 years ago, matter
is simply, "undulations in the fabric of space".
7.3 THE SIMPLE ELECTRON
The elegance of the electron structure is its basic simplicity. It is only
two spherical waves gracefully undulating around a center, each transforming
into the other. Its spherical wave structure combines with the waves of
other charged particles to create myriads of standing wave structures.
These structures become the crystalline matter of the solid state. If you
could see its wave structure, a crystal might appear like many shimmering
bubbles neatly joined in geometric arrays. The arrays are held together
with immense rigidity - a property of space.
The next frontier science of the future is to understand the meaning
and structure of space.
8. References and Further Reading
-
Apeiron, V2, No. 4, Oct. 1995. This contains eight articles discussing
various interpretations of quantum theory.
-
E. Battey-Pratt, and T. Racey (1980) "Geometric Model for Fundamental Particles,"
Intl. J. Theor. Phys. 19, 437-475. They recognized that electron
spin was a geometric property of space and could exist in a spherical structure.
-
Louis Duc de Broglie (1924), PhD thesis "Recherché sur la Theorie
des Quanta," U. of Paris. He proposed a wavelength l=h/p for the quantum
waves of an electron containing an oscillator of frequency, mc2/h.
as in the space resonance.
-
William Clifford (1956), "On the Space Theory of Matter" The World of
Mathematics , p 568, Simon & Schuster, NY. An English mathematician
at the Royal Philosophical Society, he first suggested (1876) that matter
was composed of pure waves.
-
John Cramer (1986), "The Transactional Interpretation of Quantum Mechanics",
Rev. Mod. Phys 58, 647-687. He interpreted the waves of quantum
mechanics as real, in contrast to the unreal but popular "probability
wave." He named an offer-wave (outward) and a response-wave (inward).
-
John A. Eisele (1960), Modern Quantum Mechanics with Applications to
Elementary Particle Physics . Wiley- Interscience, (John Wiley &
Sons, NY, London). This book discusses the Dirac Equation in detail.
-
C.W. Misner, K. Thorne, and J.A. Wheeler (1973), Gravitation , W.H.
Freeman Co. p1149. This book covers many pioneering ideas including the
3D space property of spherical rotation .
-
C. Rebbi (1979) "Solitons" Scientific American, Feb., 92, 168. He discusses
spherical rotation applied to Solitons.
-
Giorgi Ryazanov (1991), Proc. 1st Int'l Sakharov Conf. Phys., Moscow, May
21-31, pp. 331-375, Nova Sci. Publ., NY. He used a Wheeler-Feynman method
to deduce that Natural Laws are the response of the universe.
-
J. Wheeler and R. Feynman (1945), "Interaction with the Absorber as the
Mechanism of Radiation," Rev. Mod. Phys. 17, 157. They modeled the
electron with inward and outward waves to investigate the energy transfer
mechanism to an absorber.
-
Milo Wolff (1990), Exploring the Physics of the Unknown Universe
, ISBN 0-9627787-0-2. (Technotran Press, CA) A reader-friendly investigation
of the natural laws with applications to particles and cosmology.
-
Milo Wolff (1991), "Microphysics, Fundamental Laws and Cosmology". Proc.
1st Int'l Sakharov Conf. Phys., Moscow, May 21-31, pp. 1131-1150, Nova
Sci. Publ., NY.
-
Milo Wolff (1993), "Fundamental Laws, Microphysics and Cosmology," Physics
Essays 6, pp 181-203.
-
Milo Wolff (1995), "Beyond the Point Particle - A Wave Structure for the
Electron," Galilean Electrodynamics 6, No. 5, pp. 83-91.
-
Milo Wolff (1997A) "Exploring the Universe and the Origin of it Laws,"
Temple University Frontier Perspectives 6, No 2, pp. 44-56.
-
Milo Wolff (1997B) "The Eight-Fold Way of the Universe," Apeiron 4,
no. 4. Oct (1997).
|