This section contains mathematical descriptions of the experiments discussed in the text. ProWave is consistently applied here and offers an intuitive way to digest the equations.
A) To better describe the double slit experiment, we will need to consider the quantum state of the slits (measure which slit through which the photons pass). It is generally understood that when the particular slit of passage is known regarding each photon, the interference pattern disappears. In the right operating regime, with the screen up close, there is no interference, with the screen far away, there is interference, as seen in the two probability distributions in Fig. 1. Consider the state of a perfect transmission:
where 1,2 kets refer to the slit number. Consider now the effect of the wall containing the slits, which tells us a number based on the slit passed by the photon. The state of this system is written as
where A = Apparatus. Thus, to describe a partial effect of the apparatus, a density matrix is needed to describe the system. There is uncertainty in the wavefunction itself, as the screen is positioned at various distances from the slits.
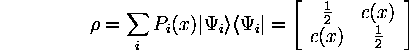
where c(x) represents the degree of coherence between the [slit] states for the wave. Using the language of QM, but with simplified equations, let our observable = B = the ``interference operator.'' Let a = ``propagation not guided by interference,'' and b = ``propagation guided by interference.'' We define B to have the following expectations:
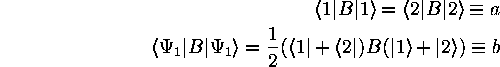
The matrix
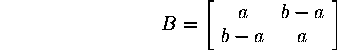
has these properties. Now, using the state 
we take a measurement:
which provides us the expectation by which many quanta produce fringes. The coefficient of `b' indicates the relative amount of interference present at the screen.
Consider the two extreme cases:
, and there is no interference.
which gives rise to the quantum coherence and so interference fringes emerge.
Interpretation: It is the present state of the system which describes the possible outcomes, not our conscious ``knowledge'' of anything regarding, say, the ``path taken by the particle.'' In this particular set-up, any photon not hitting the wall containing the slits passes through both slits. Note, a partial interaction between matter and a quantum of energy puts that quantum into a state we cannot adequately conceptualize (i.e. a reconfiguration of the energy in the wave packet), but we can only intelligently discuss probabilities of likely outcomes upon a complete interaction with matter in the case of photons.
B) Many EPR experiments involve the generation of correlated pairs of photons in an entangled state. Without loss of generality, consider as an example, the singlet state
Where x,y refer to orthogonal polarization states, and L,R label the left and right paths. The results of these experiments pioneered by Alain Aspect in 1982 confirm nonlocal effects. All the mathematics confirms this as well, but it has also been proven that these effects cannot be used to change the statistical averages of observables over distances faster than light could propagate a signal [7]. Any observable, B, which acts on one of the two sides treats this state as if each particle were in a mixture of states and not quantum correlated. Only after bringing together the data from both detectors can the patterns of quantum interference be observed. Neither side will exhibit quantum interference on its own, for example, measure any observable B on the left side:
The interference terms with innerproducts involving both x and y disappear
from the orthogonality of 
. As Fig. 2 suggests, these quanta are waves
propagating and overlapping in space. Thus, they are both present at both
detectors. The measurement of one quanta (by probablistic means) forces
the other to reconfigure opposite to the first one. When the first quantum
undergoes annihilation and transfers its energy locally, the other quantum
reconfigures as well, governed by the quantum correlation (which includes
conservation laws). Based on the equation above, by measuring the polarization
of the photon on the left, we can determine what the polarization of the
photon on the right will be if measured in the x-y basis, but we cannot
use this knowledge to send information faster-than-light.
C) The Quantum Eraser Experiment can be understood in terms of following the state functions of the correlated particles. First, let's understand how the interference is observed without the polarization rotator. With the rotator removed, the state can be expressed as
where a,b refer to the two different paths described in (Fig. 3), and 1,2 index the quanta. The beam splitter performs a unitary transformation into the A,B basis according to
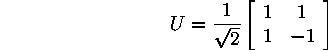
where U acts on each a,b state (and each photon) separately giving
Thus, upon leaving the beam splitter, the 2-photon state is
which indicates that the only two outcomes of a measurement are both quanta appearing at the first detector, or both at the second detector. ProWave asserts that at this point, both photons are still present at both paths A and B, like the wave function suggests, until the energy is actually transferred to the detector. This is because there is quantum coherence between these states.
Now, if we insert the polarization rotator in the `b' path, the system acquires an additional degree of freedom and is described by
Where 
and 
represent orthogonal polarization states. Next, we use this state to propagate
through the beam splitter, obtaining
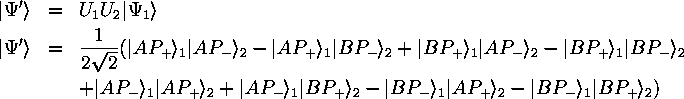
With all these terms present, it is no surprise that this state generates all combinations of detector clicks (with repeated events, of course). Each term in this state has equal likeliness of emerging upon detection.
With this same state, 
, consider putting in the two linear polarizers in front of the detectors,
oriented at 
to both beams for simplicity. These polarizers let pass the polarization
state 
and absorb the orthogonal state 
and are related to the original polarization basis by
To find out what effect these have on the state of the system, project
onto the polarizers' basis, and drop all terms that don't lead to coincidence
counts (2 photon counts). The new wavefunction now has only 
terms and is not normalized because of the dropped terms.
Thus, we have recovered the same interference effect as before by treating the wavefunction as the actual energy carried by the photons right up to the point of their demise in the detector. The state of the photons is the reality we seek, and it describes all interactions and interferences we observe with a causal relationship. The interference along all directions was always present, up till the final interaction which destroyed the photons.