ProWave offers new insights into the experiments involving quantum phenomena, and how nature can produce the results that it does. It is worthwhile to describe how the experimental results mentioned above can make sense given the ProWave view of reality. A deeper, more mathematical description of the experiments is found in the Appendix with ProWave providing a consistent, realistic explanation.
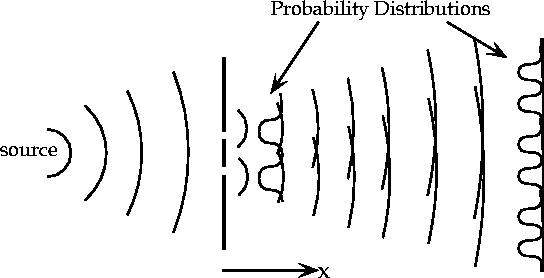
Figure 1: A typical 2 slit experiment showing probability distributions
at different distances from the slits.
In the two slit experiment (Fig. 1),
a photon enters the two slits as a single, expanding wave. At the wall,
its instantaneous probability of impacting on the surface of the wall is
quite high. In the event that it makes it through the slits, the wave at
the walls disappears and all the energy is collected and passes through
the slits. This is governed by the quantum mechanical probability of absorption
of the wall. As the wave now interferes with itself upon passing through
the slits and propagating some distance to allow overlap, the energy of
the quantum is spread out according to its probability distribution function
( 
). Absorption of the photon, now, is a local process governed again by
probability. Once the probability distribution collapses, the ``balloon
pops'' everywhere and the quanta of energy localizes at the point of transfer.
This localization need not occur instantaneously, and it makes sense to
conceive of it occurring on the timescale of energy absorption. As of today,
this notion does not violate any laws of physics because there currently
is no description of how a photon's probability distribution collapses
upon absorption.
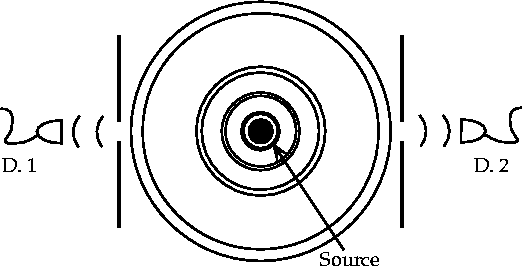
Figure 2: An experiment with EPR correlated particles.
I think the key to understanding any of the EPR correlations (Fig.\ 2) is to forego the idea that two distinct particles are emitted from some source in opposite directions. Quantum mechanics treats them as indistinguishable and as both being emitted in both directions, so let's treat them that way physically. The sources typically do not prefer a direction upon emission, making the correlated photons themselves spherical waves propagating, overlapping each other (one field). Any effect on one wave has a direct effect on the other wave as well. Thus, say, if a particle is measured at one location (a photon was absorbed locally), then its partner snaps into a state opposite the source and resumes propagation. Analogously, imagine two balloons expanding together with the same radius. If one balloon pops, that causes the other to reconfigure as well. The reconfiguring of the second photon could be conceived of to have occurred instantaneously, but the final act of localization for energy transfer need not be. Again, this is consistent with what is known from QM about spin, polarization, and momentum correlations.
The quantum erasure experiment (Fig. 3)
described in Section III is nothing other than a ``directional interference''
effect. No future activities or consciousness effects are needed to explain
this experiment. The correlated pair is emitted as two quanta overlapping
each other. They interfere at the splitter and the effects are detected.
When one path undergoes polarization rotation, we no longer observe the
interference of the two paths. This is no surprise because one path has
polarization x and one has polarization y, and these are orthogonal. However,
both x and y polarizations have a component of polarization in the z direction.
These z-components do interfere at the beam splitter and the effect can
be observed by putting in a linear polarizer oriented in the z direction
directly in front of each detector. Note that the z-polarizer effectively
filters out the orthogonal 
interference which can cancel the z-component interference. In essence,
all of these interference effects are present until the complete interaction.
The type of interference that is manifested and becomes visible is a function
of how the detectors are set up.
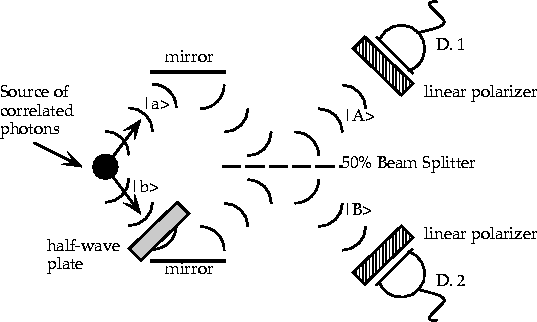
Figure 3: The quantum eraser experiment.